What is the Sharpe Ratio?

The Sharpe Ratio, also known as the Sharpe Index, was proposed by William Sharpe in 1966. Professor Sharpe derived a formula which compares the return on investment and its associated risk. The Sharpe Index shows a trade-off between risk and return of an investment or a portfolio.  

Investors use the Sharpe ratio to understand the performance of a share or their portfolio. Investors also use the Sharpe ratio to compare numerous funds with similar risk-return profiles.

To calculate the Sharpe Ratio, the risk premium of a security or portfolio is divided by the standard deviation of that fund or portfolio.   

Formula:

Sharpe Ratio

= (Return of the portfolio – Return of Risk-Free Asset)/ Standard Deviation of Portfolio

Symbolic Representation:

Sharpe Ratio

= (Rp – Rf)/ σp

• Return of the Portfolio: A portfolio’s return is the total performance of all the investments; it represents the total profit or loss that is produced over a certain period. It is a crucial metric that investors use to understand how well their investment plan is working and how well the portfolio can achieve their financial goals.
• Risk-Free Rate: The risk-free rate is a theoretical rate of return earned on risk-free assets. The return on these risk-free assets is the minimum return, and in many risk-return assessments, the risk-free rate acts as the base. Example: Government bonds or Treasury Bills can be a good benchmark.
• Standard Deviation of Portfolio: Standard Deviation is a statistical tool which measures the degree of fluctuation between an individual value and the mean of a probability distribution. In the investment frontier, the standard deviation measures the risk and volatility of an investment or portfolio. It showcases the variability of the return from the principal return of the investment. It is crucial to know that the lower the standard deviation, the lower the risk, and the higher the standard deviation, the greater the risk. Depending upon the standard deviation, the Sharpe ratio also fluctuates. If the standard deviation is more, the Sharpe ratio will be high. If the standard deviation is low, the Sharpe ratio will be high.

Market Risk Premium: When we subtract a risk-free return from the expected return of a security, we get a risk premium. The risk premium helps investors evaluate potential investments by understanding the extra return earned for the additional risk taken. The risk premium is the extra return on investment earned for taking additional risk compared to a risk-free investment.

Risk Premium

= Return of the portfolio – Return of Risk Free Asset

Sharpe Ratio’s Threshold:

Investors use the Sharpe ratio to grade a company before making investment decisions.

• A Sharpe ratio of less than (>) 1 is considered poor for investment purposes. 
• A ratio scaling between 1 – 1.99 is considered adequate. 
• The Sharpe index is between 2 and 2.99, which investors interpret as very good. 
• And if the Sharpe ratio is above 3, it is viewed as excellent.      

Real-Life Example of Sharpe Ratio

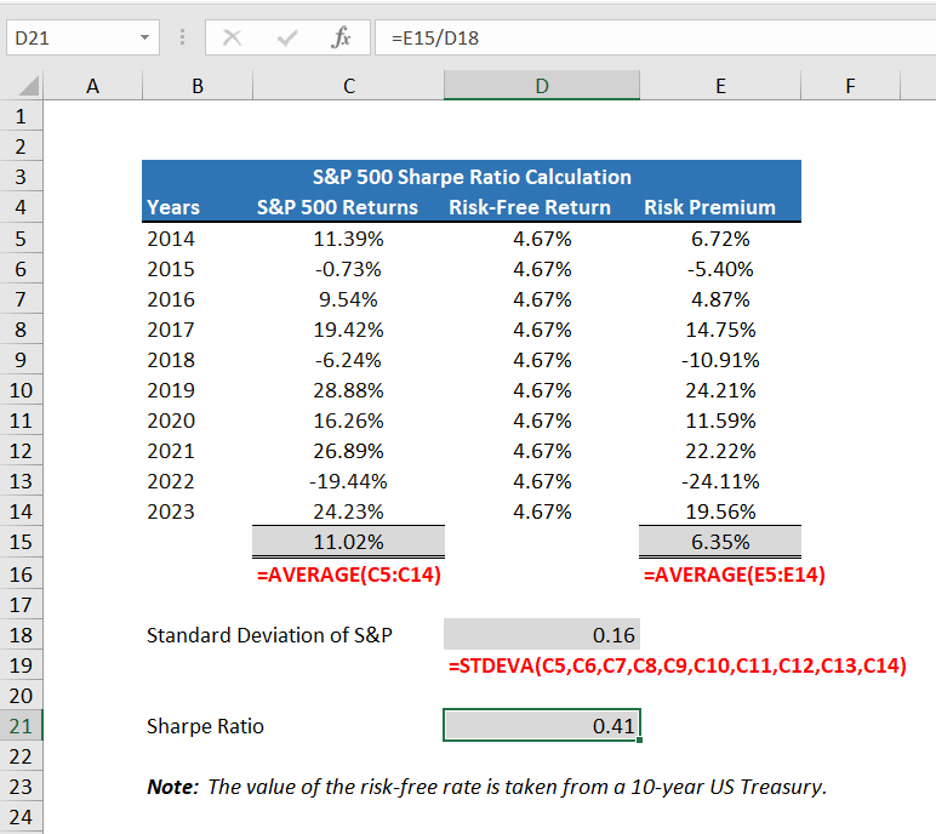
Let’s understand the calculation of the Sharpe ratio of the S&P 500 from 2014 to 2023:

Sources:

• S&P 500 Returns: https://ycharts.com/indicators/sp_500_return_annual#:~:text=Basic%20Info-,S%26P%20500%20Annual%20Return%20is%20at%2024.23%25%2C%20compared%20to%20%2D,holding%20the%20S%26P%20500%20index.
• 10-year US Treasury Rate: https://ycharts.com/indicators/10_year_treasury_rate#:~:text=Basic%20Info,day%20and%203.44%25%20last%20year.

For the calculation, we have taken the S&P 500 returns of 10 years i.e. from 2014 to 2023. These returns are recorded on 31st December of every year. We are considering the present rate of a 10-year US Treasury for the risk-free rate.

In the table, the first column shows the periods. Followed by annual returns of the S&P 500 in the second column. In the third column, we have recorded the 10-year UD treasury rate. We use the same 10-year US treasury rate to calculate the risk premium for all 10 years. In the last column, we have calculated the risk premium or excess return earned by subtracting the risk-free rate from the S&P 500 return.

Sharpe Ratio

= (Return of the portfolio – Return of Risk-Free Asset)/ Standard Deviation of Portfolio

In cell E15, we calculated the average risk premium by using the =AVERAGE(E5:E14) Excel formula. With this, we have computed the numerator of the Sharpe ratio of 6.35%.

For the denominator, we have to calculate the standard deviation of the S&P 500 returns for all 10 years. In cell D18 we have calculated the standard deviation using the =STDEVA formula as 0.16.

In cell D21 the final calculation of Sharpe ratio is performed. We have divided the average risk premium with the standard deviation of the S&P 500 to get the Sharpe ratio as 0.41.     

Time Dependency 

The Sharpe ratio is a widely used risk-adjusted return. It exhibits time dependency due to its sensitivity to changes in both returns and risk over time. The following factors result in the fluctuations in the Sharpe ratio:

• The Sharpe ratio can be high and unstable in the short term, as it may be affected by volatility in asset prices and market conditions. Even small fluctuations in returns or risk can significantly impact the Sharpe ratio, leading to different interpretations of risk-adjusted performance over various time frames.
• Changes in market conditions and seasonal trends can impact the Sharpe ratio’s performance over time. The Sharpe ratio may fluctuate during market volatility or economic uncertainty, reflecting changes in risk perceptions and investor sentiment. The impact of bull and bear market cycles on the Sharpe ratio can also cause risk-adjusted returns to vary, depending on market conditions.
• The Sharpe ratio of a portfolio may vary over time due to portfolio rebalancing or changes in asset allocation. As investors adjust their long term investments strategies or reallocate assets in response to changing market conditions or investment objectives, the portfolio’s risk-return profile may evolve. This evolution can lead to changes in the Sharpe ratio over time.

Applications of the Sharpe Index:

Investors use the Sharpe Ratio or Index for various aspects. A few of them are as follows:

• Investors use the Sharpe Ratio to measure the risk-adjusted performance of the portfolio or securities.
• As the Sharpe ratio provides meaning only when it is compared with benchmarks or other securities, it gives investors the Sharpe index to compare various investment avenues. 
• Sharpe ratio helps investors to identify and rank assets based on their risk-return profile. With this, investors can rank and evaluate securities based on their performances. 
• Investors can use the Sharpe ratio to define investing goals and assess their risk tolerance. Investors can establish clear performance benchmarks and assess whether their investments are meeting their targeted risk-adjusted returns by setting a target Sharpe ratio for their portfolio.
• The Sharpe ratio is a tool used by portfolio managers to track and control portfolio risk. Portfolio managers can evaluate the success of their investing strategies, modify portfolio allocations, and reduce excessive risk exposure by monitoring changes in the Sharpe ratio over time.

Conclusion  

The Sharpe Ratio, devised by William Sharpe, stands as a pivotal measure for evaluating the risk-adjusted performance of investments. By quantifying the trade-off between risk and return, investors harness its power to discern the effectiveness of portfolios or securities, enabling informed comparisons and strategic decision-making. Its role extends to setting investment goals, benchmarking performance, and guiding risk management strategies. Moreover, the Sharpe Ratio’s sensitivity to market fluctuations underscores its dynamic nature, emphasising the need for vigilant monitoring and adaptive portfolio management. Ultimately, it is an indispensable tool for investors and portfolio managers navigating the complexities of financial markets.