Bonds represent one of the most fundamental investment options in finance. Investors, corporations, and governments rely on bonds for capital and stability. Understanding how bonds are priced is crucial for making informed investment decisions. Bond pricing model is the present value of expected future cash flows discounted at an appropriate rate. This article delves into the bond pricing model, its components, and its practical implications for investors.
WHAT IS BOND PRICING MODEL?
Bond pricing is a discounted cash flow (DCF) exercise at its core. The value of a bond (denoted as IV₀) is determined by discounting the bond’s future cash flows—comprising coupon payments and the principal amount—back to the present using a required rate of return which is the cost of debt based on credit rating (Kd). This discounting process reflects the time value of money, where a dollar today is worth more than a dollar in the future.
In other words,
IVo: Present value (PV) of future cash flows discounted at Cost of Debt based on credit rating (Kd).
Kd: The yield required by investors, often derived from the cost of debt based on credit rating of similar bonds in the market.
Future Cash Flows: Includes periodic coupon payments and the bond’s face value (principal) at maturity.
And Po: Current price of the bond that is used to calculate the Yield to maturity(YTM) of the bond.
where, YTM: Return an investor will earn if they hold the bond to maturity.
APPLICATION IN DIFFERENT TYPES OF BONDS
The application of bond pricing in different types of bonds shall be as follows:
1. ZERO COUPON BOND (ZCB): These bonds do not provide periodic coupon payments. Rather, they are issued at a significant discount and redeem at their full face value upon maturity. The intrinsic value of a ZCB is calculated as:
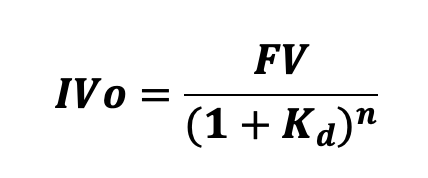
where FV is the face value, Kd is the cost of debt and n is the number of years to maturity.
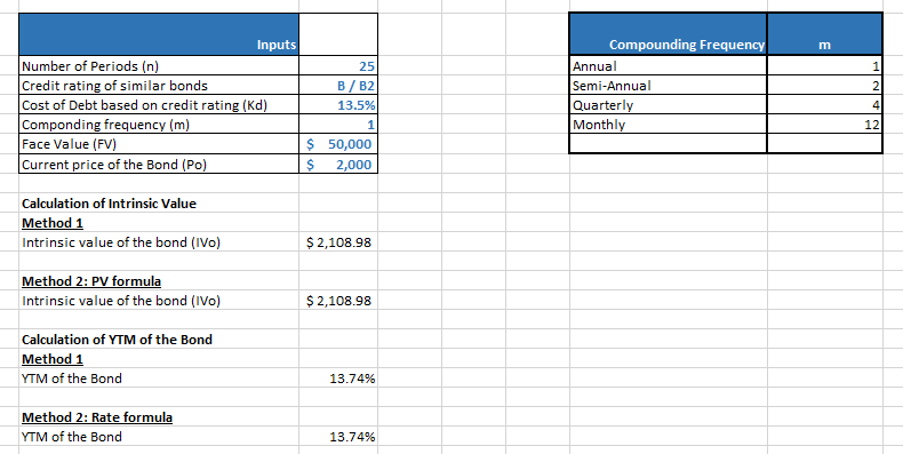
For example, consider a 25-year-deep discount bond with a face value of $50000. If the cost of debt based on credit rating of similar bond (let’s assume credit rating B/B2) is 13.5% p.a., the bond’s intrinsic value can be calculated as follows (assuming annual compounding):
Method 1: Formula based
IVo = $50000 / (1+13.5%)^25
= $2,108.98
Method 2: PV function
We can also calculate the intrinsic value of the bond using the PV function in Excel where the syntax is as follows:
IVo= PV(rate/m, nper*m, pmt/m, [fv], [type])
Where, rate = Cost of Debt (Kd)
Nper= number of period (n)
Pmt = Periodic payment (C* FV)
FV = Future Value
m = Compounding frequency
IVo = PV (Kd/m, n*m, 0, -FV)
= PV (13.5%, 25, 0, -50,000)
= $2018.98
Similarly, we can also value a bond by calculating its YTM given the current price of the bond (Po) and other variables as above.
YIELD TO MATURITY CALCULATION – ZERO COUPON BOND
For example, for the above bond we also have the current price of the bond as $2000. We can compute the yield to maturity (YTM) as follows:
Method 1: Formula based
YTM= (FV/Po) ^ (1/n)-1
= (50,000/2,000)^(1/25)-1
= 13.74%
Method 2: PV function
YTM = RATE(nper*m, pmt, pv, [fv], [type], [guess])*m
Where, Nper= number of period (n)
Pmt = Periodic payment (C* FV)
PV = Present value i.e., the current price (Po)
FV = Future Value
m = Compounding frequency
YTM = RATE(n*m, 0, Po, -FV)*m
= RATE(25*1, 0, 2000, -50000)*1
= 13.74%
We have modelled the same example in an Excel file where we can change our inputs and check results for different zero-coupon bonds with different compounding frequencies and different credit ratings.
**
2) PERPETUAL BOND: These bonds pay fixed coupon payments indefinitely and do not have a maturity date. The value of a perpetual bond is determined using the following formula:
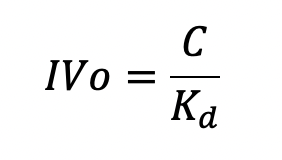
where C is the Coupon amount and Kd is the cost of debt of bonds with similar credit rating.
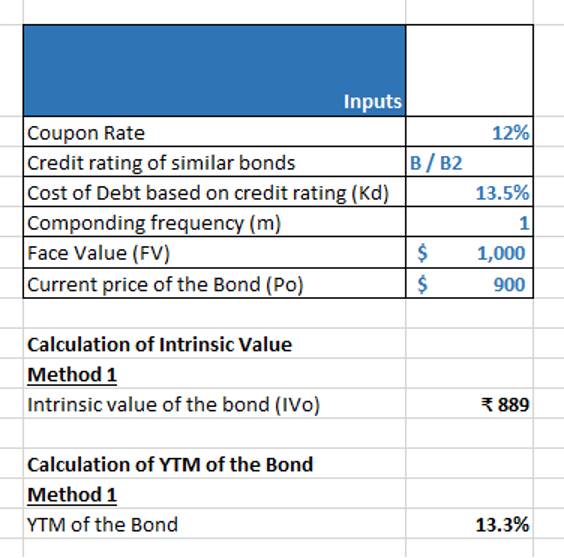
For example, for a Perpetual bond of face value (FV) of $1000 and coupon rate of 14%, the yield in the market on similar bonds (assume the bond is having credit rating of B/B2) is 13.5%, its intrinsic value can be calculated as follows (assuming annual compounding):
Method 1: Formula based
IVo = $14%*$1000 / 13.5%
= $889
Similarly, we can also value a bond by calculating its YTM given the current price of the bond (Po) and other variables as above.
For example, in the above example the current price of the bond (Po) is given as $900 and rest of the variables are same. We can calculate the YTM of the bond as follows:
YIELD TO MATURITY CALCULATION – PERPETUAL BOND
Method 1: Formula based
YTM = (Coupon Rate * Face Value of Bond) / Current price of the Bond
= (12% * $1000)/ $900
= 13.3%
We have modelled the same example in an Excel file where we can change our inputs and check results for different perpetual bonds with different compounding frequencies and different credit ratings.
**
3) CONVENTIONAL OR PLAIN VANILLA BOND: These bonds offer a fixed coupon rate every year until maturity, which is subject to one-shot bullet redemption. The pricing follows the standard bond pricing formula as follows:
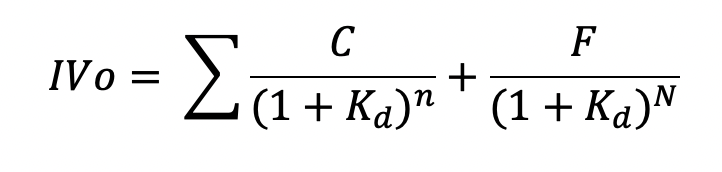
where C is the coupon amount, F is the face value, Kd is the cost of debt based on bonds with similar credit rating and N is the years to maturity.
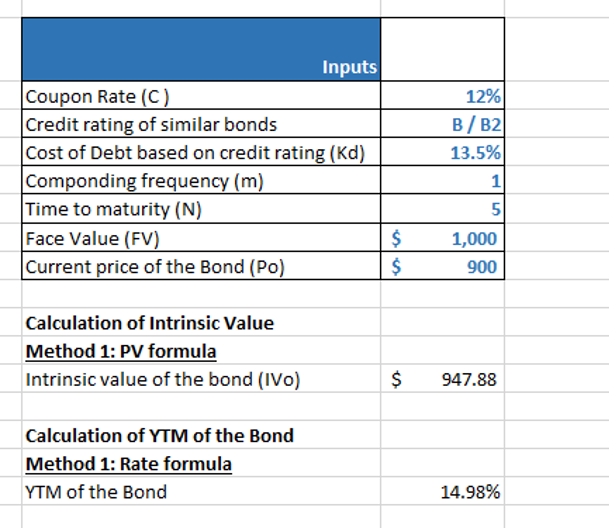
For example, an investor considers purchasing a 5-year plain vanilla bond with a face value of $1,000, an annual coupon of $120 (12% coupon rate), and cost of debt (assuming credit rating B/B2) as 13.5%. The bond price is calculated (assuming compounded annually) as follows:
Method 1: Formula based
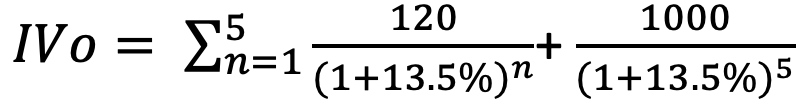
= 120/(1+13.5%)^1 + 120/(1+13.5%)^2 + 120/(1+13.5%)^3 + 120/(1+13.5%)^4 + 120/(1+13.5%)^5 + 1000/(1+13.5%)^5
= $105.73 + $93.15 + $82.07 + $72.31 + $63.71 + $530.91
= $947.88
Method 2: PV function
We can also calculate the intrinsic value of the bond using the PV function in Excel where the syntax is as follows:
IVo= PV(rate/m, nper*m, pmt/m, [fv], [type])
Where, rate = Cost of Debt (Kd)
Nper= number of period (n)
Pmt = Periodic payment (C* FV)
FV = Future Value
m = Compounding frequency
IVo = PV (Kd/m, n*m, (C*FV)/m, -FV)
= PV (13.5%, 25, (12%*1000), -50,000)
= $947.88
Similarly, we can also value a bond by calculating its YTM given the current price of the bond (Po) and other variables as above.
For example, for the above bond we also have the current price of the bond as $900. We can compute the yield to maturity (YTM) as follows:
YIELD TO MATURITY – CONVENTIONAL BOND
Method 1: RATE function
YTM = RATE(nper*m, pmt, pv, [fv], [type], [guess])*m
Where, Nper= number of period (n)
Pmt = Periodic payment (C* FV)
PV = Present value i.e., the current price (Po)
FV = Future Value
m = Compounding frequency
YTM = RATE(n*m, 0, -Po, FV)*m
= RATE(5*1, (12%* 1000)/1, -900, 1000)*1
= 14.98%
We have modelled the same example in an Excel file where we can change our inputs and check results for different zero-coupon bonds with different compounding frequencies and different credit ratings.
**
4) NON-CONVENTIONAL BOND: These are bonds with unique structures that deviate from standard bond types. Examples include step-up bonds, convertible bonds, and callable bonds. The pricing of these bonds depends on additional factors such as embedded options or variable interest rates.
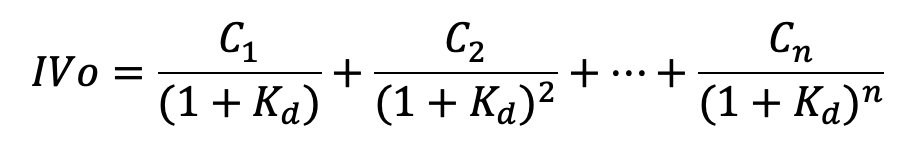
Example 1: We have a step-up bond with a face value of $1,000, maturity of 5 years, 13.5% as the cost of debt (assuming the bond has credit rating B/B2) and step-up coupon rates as follows:
| Years | Rate |
| 1 | 5% |
| 2 | 6% |
| 3 | 7% |
| 4 | 8% |
| 5 | 9% |
Given the above details we can calculate the intrinsic value of the Bond (assuming annual compounding) as follows:
Method 1: Formula based
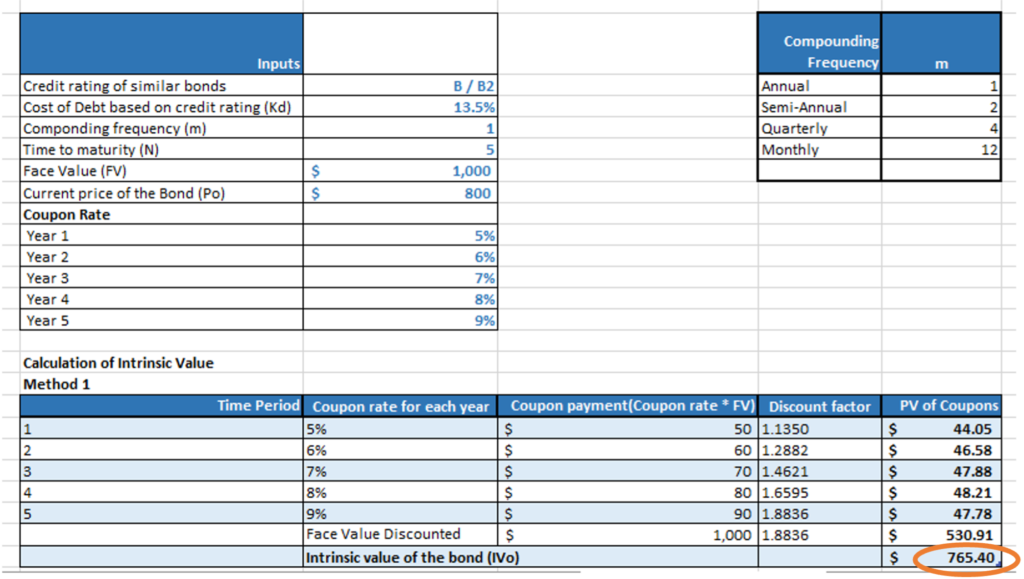
The value of the bond comes to $765.40.
Method 2: NPV function
We can also calculate the IVo of the bond using the NPV function in Excel.
IVo =NPV(discount_rate, value1, [value2], …)
Where, discount rate = Cost of Debt (Kd)
Value = Cash flows comprising the coupon and the redemption of the Face value
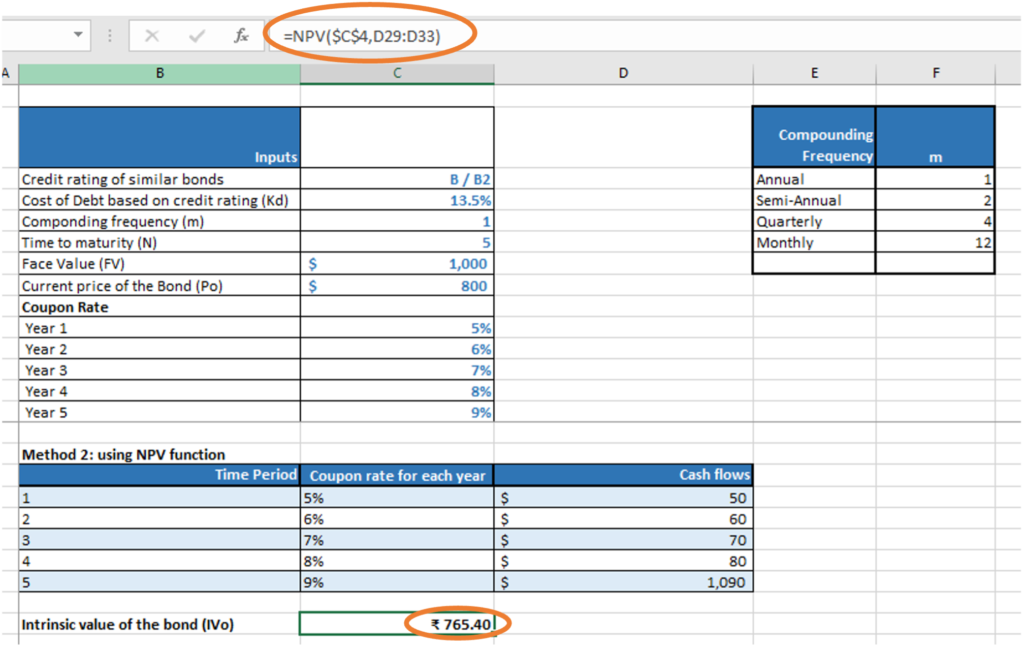
Note, we get the same value of the bond as $765.4 with the NPV function in Excel also.
Similarly, we can also value a bond by calculating its YTM given the current price of the bond (Po) and other variables as above.
YIELD TO MATURITY – NON-CONVENTIONAL BOND
For example, for the above bond we also have the current price of the bond as $800. We can compute the yield to maturity (YTM) as follows:
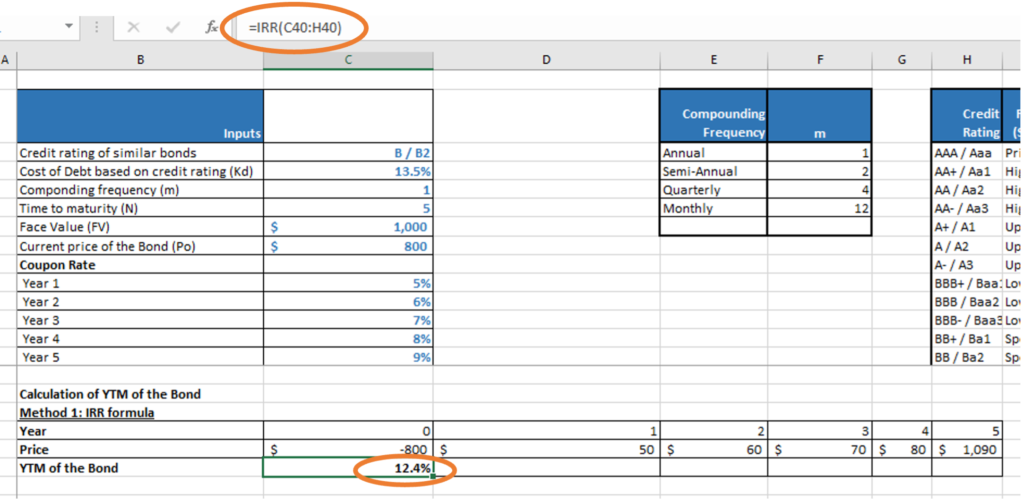
Method 1: IRR function
YTM = =IRR(values, [guess])
Where, Values = Cash flows and outflows i.e., the current price and the cash flows and redemption to be received in the future.
**
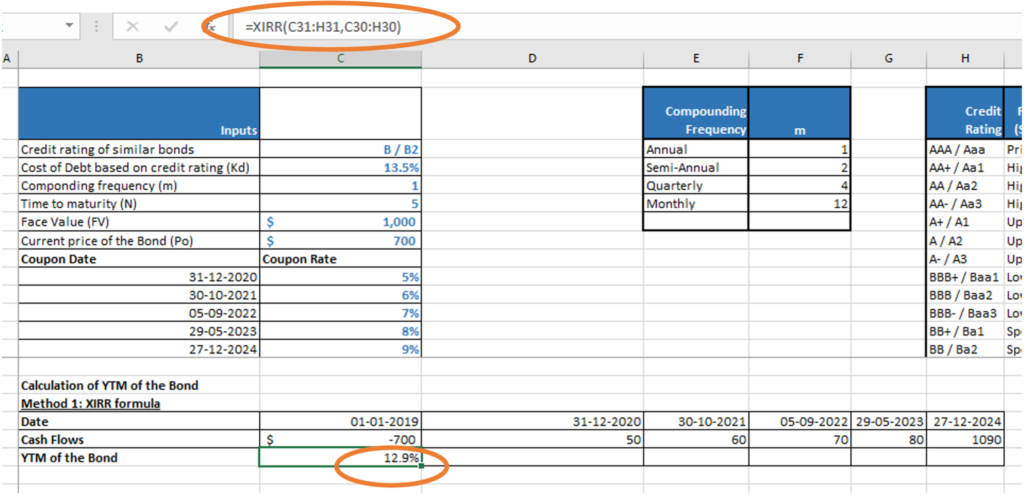
Example 2 (Non-Conventional Bond): We have a step-up bond with a face value of $1,000, maturity of 5 years, 13.5% as the cost of debt (assuming the bond has credit rating B/B2). The coupon is paid on different dates each year and step-up coupon rates are as follows:
| Coupon Date | Coupon Rate |
| 31-12-2020 | 5% |
| 30-10-2021 | 6% |
| 05-09-2022 | 7% |
| 29-05-2023 | 8% |
| 27-12-2024 | 9% |
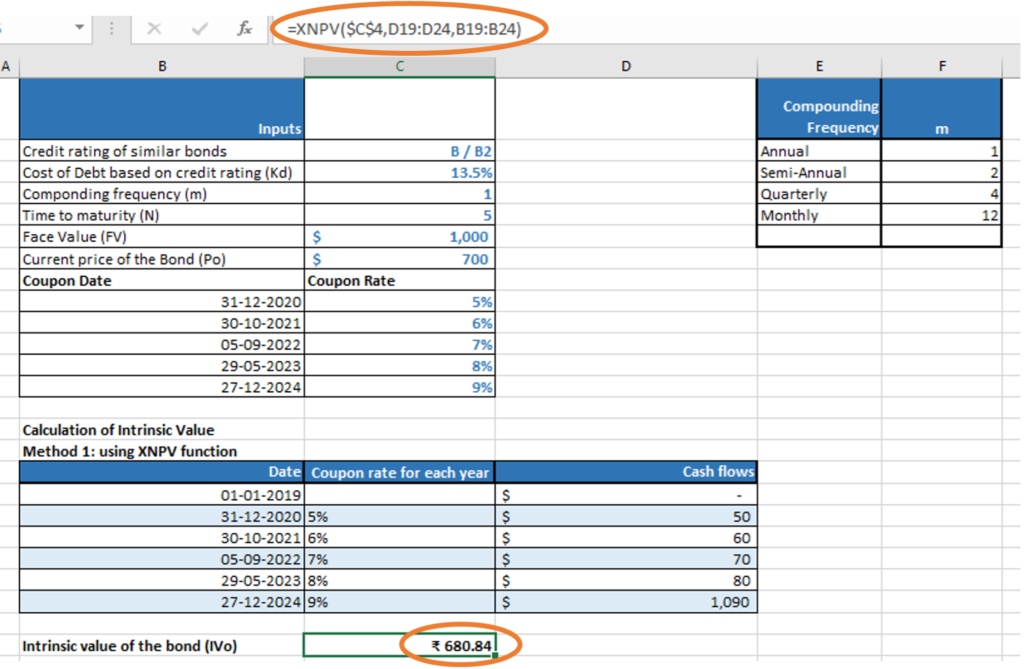
Given the above details, we can calculate the intrinsic value of the Bond using the XNPV function in Excel.
Method 1: XNPV function
IVo =XNPV(rate, values, dates)
Where, rate = cost of debt (Kd)
Values = Cash flows comprising the coupon and the redemption of the Face value
Dates = Range of dates on which coupon is paid or Face value is redeemed
Similarly, we can also value a bond by calculating its YTM given the current price of the bond (Po) and other variables as above.
For example, for the above bond we also have the current price of the bond as $700. We can compute the yield to maturity (YTM) as follows:
Method 1: IRR function
YTM = XIRR(values, dates, [guess])
Where, Values = Cash flows and outflows i.e., the current price and the cash flows and redemption to be received in the future.
Dates = range of dates on which the current price is paid and cash flows occur
**
RELATIONSHIP BETWEEN PVo, IVo, Kd, AND YTM
The bond’s price (PVo) and intrinsic value (IVo) play a key role in guiding bond investment decisions. The required rate of return or cost of debt based on credit rating of similar bonds (Kd) represents the minimum return investors expect, considering the bond’s risk and prevailing market conditions. In contrast, the yield to maturity (YTM) reflects the actual return an investor can achieve by holding the bond until it matures. When YTM is higher than Kd, the bond price (PVo) falls below its intrinsic value (IVo), making it an attractive buy. Conversely, when YTM is lower than Kd, the bond price exceeds its intrinsic value, indicating overvaluation. The bond market continuously adjusts prices to reflect the changing relationship between YTM and Kd, affecting investment strategies.
BOND PRICING SCENARIOS
The price of a bond is influenced by market conditions and the relationship between the bond’s yield and the required rate of return or cost of debt based on credit rating. The three main cases include:
- Case 1: P₀ < IV or YTM > Kd
When the bond’s market price (Po) is below its intrinsic value (IVo), the bond is undervalued. Investors should capitalize on this opportunity by buying the bond, as it is likely to generate superior returns. For such bonds YTM > Kd.
- Case 2: P₀ > IV or YTM < Kd
If the bond’s market price (Po) exceeds its intrinsic value (IVo), it is considered overvalued. Investors may choose to sell or short such bonds to avoid losses or profit from potential price corrections. For such bonds YTM < Kd.
- Case 3: P₀ = IV or YTM = Kd
Here, the bond is fairly priced, meaning its market price (Po) accurately reflects its intrinsic value (IVo). Investors may choose to hold the bond, as there is no immediate incentive to buy or sell. For such bonds YTM = Kd.
CONCLUSION
Understanding bond pricing model is essential for fixed-income investors looking to navigate the bond market with confidence and precision. By mastering the formula and leveraging tools like Excel models, investors can bridge the gap between theory and practice, evaluating opportunities ranging from corporate bonds (like bonds of Apple Inc. or Netflix) to government treasuries. This knowledge empowers investors to optimize portfolio composition, assess risks, and seize market opportunities—such as purchasing discounted bonds during rising interest rate environments or benefiting from price gains when rates decline.


