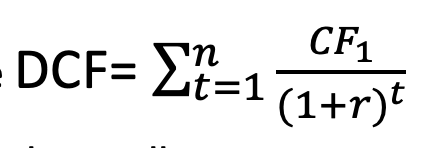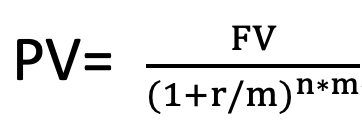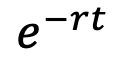Ever wondered how to figure out what a future sum of money is worth today? This is where the concept of Present Value (PV) meets the time value of money. The saying “a dollar today holds more value than a dollar tomorrow” perfectly encapsulates this concept. But how exactly do you calculate the value of money over time? Present Value calculator are essential tools for investors and analysts to determine this. So, what is PV, and how do these calculators help explain the time value of money? Let’s dive in!
PRESENT VALUE: THE KEY TO UNDERSTANDING THE TRUE WORTH OF MONEY
In finance, Present Value (PV) is crucial for determining the real worth of future cash flows in today’s terms. Rooted in the Time Value of Money (TVM), PV highlights that a dollar today is more valuable than a dollar in the future. This is because money can grow if invested, while inflation and other risks can erode its future value.
At its core, PV represents the current worth of future cash flows, discounted back to today using a specific interest rate. This discounting accounts for the risks and opportunity costs of waiting. For example, consider inflation: if you’re set to receive $1,000 five years from now, and inflation is projected at 3% per year, that future amount will have less purchasing power—essentially worth only about $863 in today’s dollars. This shows how inflation diminishes the value of cash received later.
Opportunity cost also plays a significant role. If you have the option to invest $1,000 today at a 5% return, in five years, that amount would grow to $1,276. However, if you choose to wait for the same $1,000 five years down the line, you miss out on that potential gain.
In short, Present Value allows businesses and individuals to evaluate the true value of future cash, guiding smarter investments and financial planning while emphasizing the importance of accounting for inflation and opportunity costs.
FORMULA TO CALCULATE THE PRESENT VALUE
Present Value (PV) is calculated by considering three key inputs: the discount rate, the time period, and the future value of cash flows. The formula for PV is:
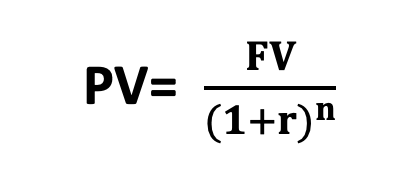
Where,
- FV= It is the Future value i.e., the estimated amount of cash expected to be received at a future date. It’s the sum we discount back to the present to determine its current worth.
- r = It represents the discount rate, which is the expected rate of return or interest. This rate is tied to the level of risk associated with the cash flow—higher risk leads to a higher discount rate.
- n = It represents the number of periods which indicates the period between when the cash flow will occur and today. This is calculated by multiplying the number of years by the compounding frequency.
Note – You can download the Present Value Calculator to practice the examples illustrated below:
Example 1:
If you’re expecting to receive $1,000 in three years with a 6% discount rate, by plugging in the inputs in the above formula we get the present value as follows:
PV = $1,000/ (1+0.06) ^3 = $839.62
Similarly, in corporate finance, it is very common to find the valuation or present value of a project, business, or investment using the discounted cash flow method and find the net present value. The formula to calculate the present value of the future stream of cash flows arising from a project is as follows:
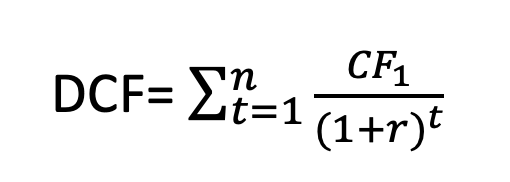
However, if one wants to know how much a project or investment is worth the investment made, one has to calculate the Net Present Value (NPV) of the project or investment. NPV is the present value of all the project’s inflows and outflows. Investment in any project is recommended only if the NPV is positive, i.e., the present value of all inflows is greater than the outflows.
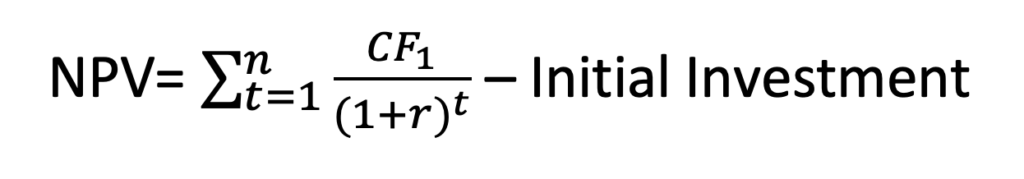
Let’s study an example of this.
Example 2:
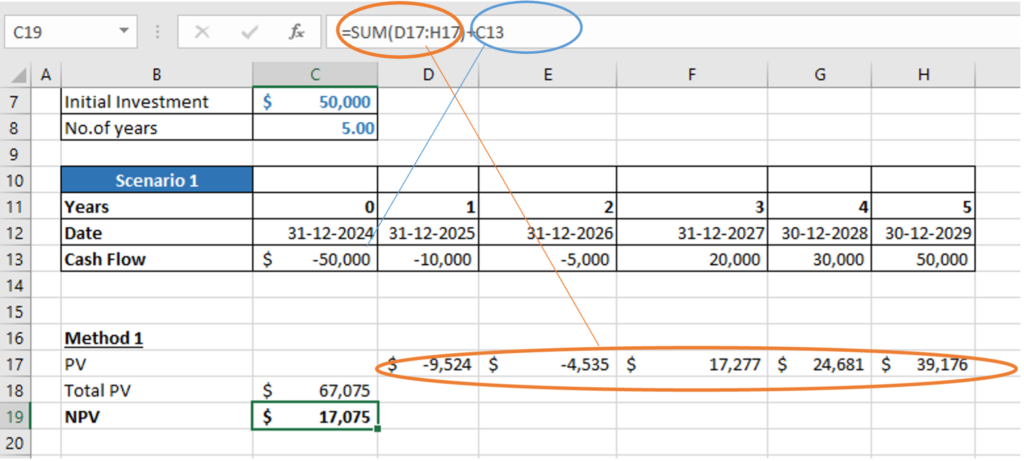
A company is evaluating an investment in a renewable energy project with an upfront cost. The project has both challenges and growth potential, and the company is keen to determine if the future cash flows justify the initial outlay. In this scenario, the company expects initial cash outflows due to high setup costs in the first two years, followed by cash inflows over the next several years as the project gains traction. However, they need to consider two possible outcomes: one where the company picks up the market fast and has high cash inflows in the first three years, and the second where a new competitor enters the market and the cash inflows are not as high due to competition in the market. The initial investment in year 0 is $50,000 and the discount rate is 5%. The projected cash flows for 5 years in both scenarios are as follows.
| Years | 0 | 1 | 2 | 3 | 4 | 5 |
| Date | 31-12-2024 | 31-12-2025 | 31-12- 2026 | 31-12- 2027 | 30-12-2028 | 30-12-2029 |
| Cash Flow (Scenario 1) | -50,000 | -10,000 | -5,000 | 20,000 | 30,000 | 50,000 |
| Cash Flow (Scenario 2) | -50,000 | -10,000 | -5,000 | 8,000 | 10,000 | 12,000 |
Present Value calculated using the Discounted Cash Flow for Scenario 1
= -10,000/(1+0.05)^1 – 5000/(1+0.05)^2 + 20,000/(1+0.05)^3 + 30,000/(1+0.05)^4 + 50,000/(1+0.05)^5
= $67,075.18
NPV = Present Value- Initial Investment
= $67,075.18 – $50,000
= $17,075.18
The cash inflows in the first three years are sufficient to cover the initial investment and expenses in the first two years at a discount rate of 5% in the first scenario.
Present Value calculated using the Discounted Cash Flow for Scenario 2
= -10,000/(1+0.05)^1 – 5000/(1+0.05)^2 + 8,000/(1+0.05)^3 + 10,000/(1+0.05)^4 + 12,000/(1+0.05)^5
= $10,481.08
NPV = Present value – Initial Investment
= $10,481.08 – $50,000
= -$39,518.92
The cash inflows in the first three years are not sufficient to cover the initial investment and expenses in the first two years at a discount rate of 5% in the first scenario.
Based on the above the managers can make the decision whether to invest in the project or not given the two scenarios above. Managers can also adjust the discount rate above to see at what rate the NPV is positive in both cases or plan certain measures to increase the cash flow in the second scenario to make the cash flow positive.
FINDING PRESENT VALUE AND NET PRESENT VALUE USING EXCEL FORMULAS
Calculating the present value (PV) and net present value (NPV) in Excel streamlines decision-making by quickly assessing cash flow values over time.
For PV calculations, Excel’s =PV(rate, nper, pmt, [fv], [type]) formula estimates the current worth of a future sum by factoring in the discount rate, periods, and any ongoing payments (PMT). In capital budgeting, NPV adds each cash flow’s present value over multiple periods.
Using =NPV(rate, range), Excel discounts a series of cash flows, beginning from the second period onward, to return the NPV. By simply inputting a rate and a range of cash flows, this formula reveals whether a project meets financial thresholds by offering a quick snapshot of value today, accounting for both positive inflows and negative outflows.
For projects with irregular cash flows and dates, Excel’s =XNPV(rate, cash flows, dates) formula provides a more precise solution by discounting each cash flow to its exact date. This is particularly useful when cash flows are not evenly spaced, as it incorporates specific time gaps between inflows and outflows. By inputting a discount rate, corresponding cash flow values, and dates, the XNPV function delivers a reliable and accurate measure of a project’s net present value, making it an indispensable tool for evaluating investments with uneven cash flow timings.
In Example 1 discussed in the article on PV calculation, the result we get from the excel calculator is as follows.
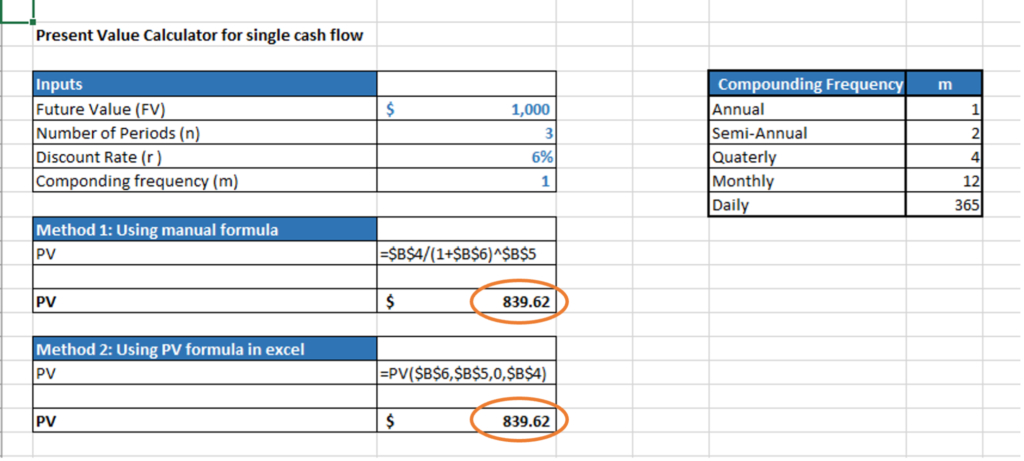
As you can see above, by using both the manual formula as well as the PV function in Excel, we get to the same Present Value of $839.62.
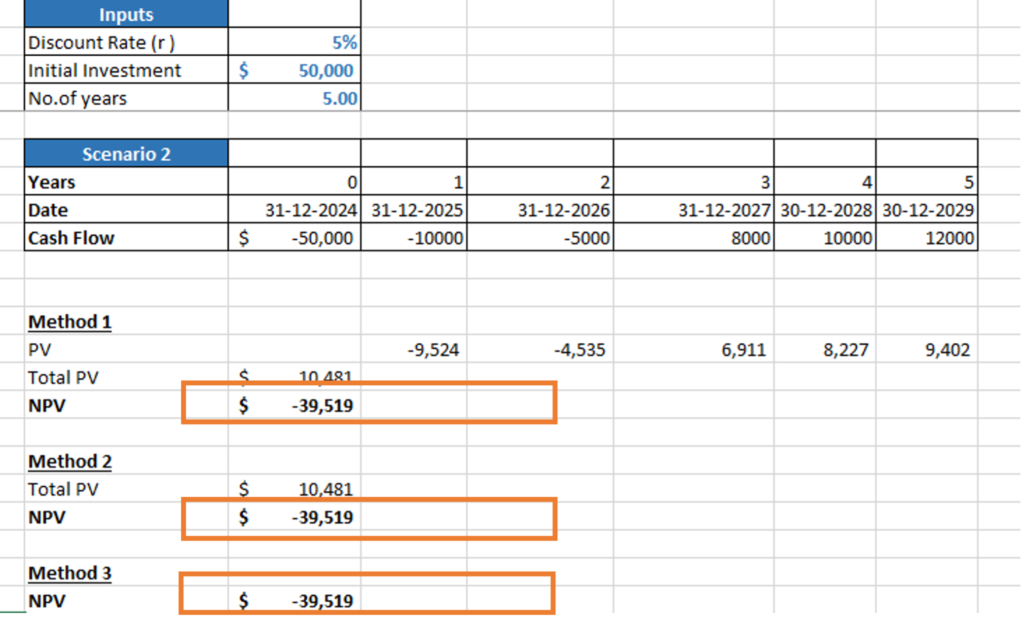
In our above Example 2 NPV can be calculated using 3 different methods in Excel for both scenarios.
Method 1: By discounting each year’s Cash flow by the
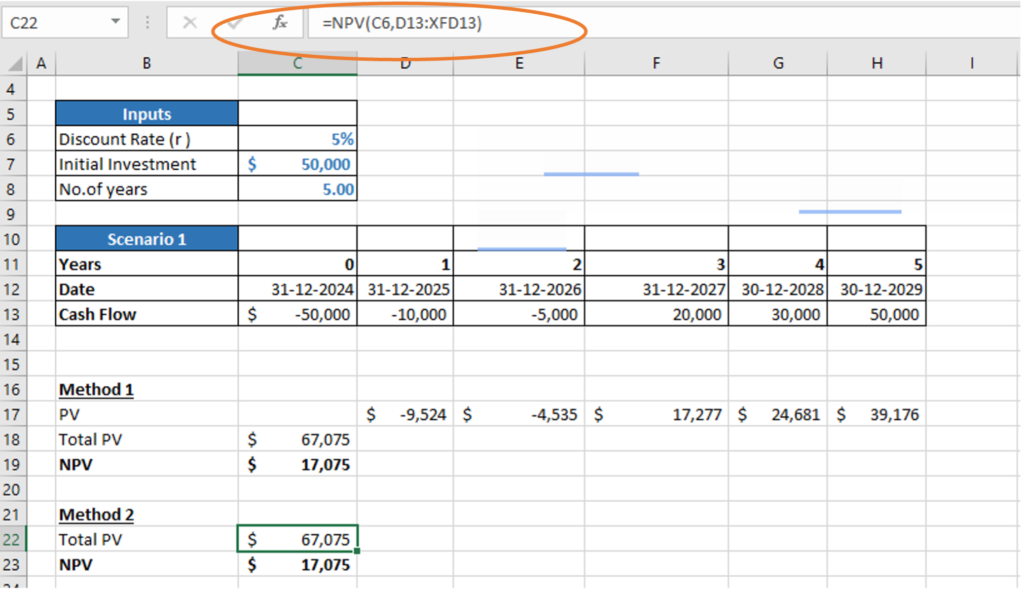
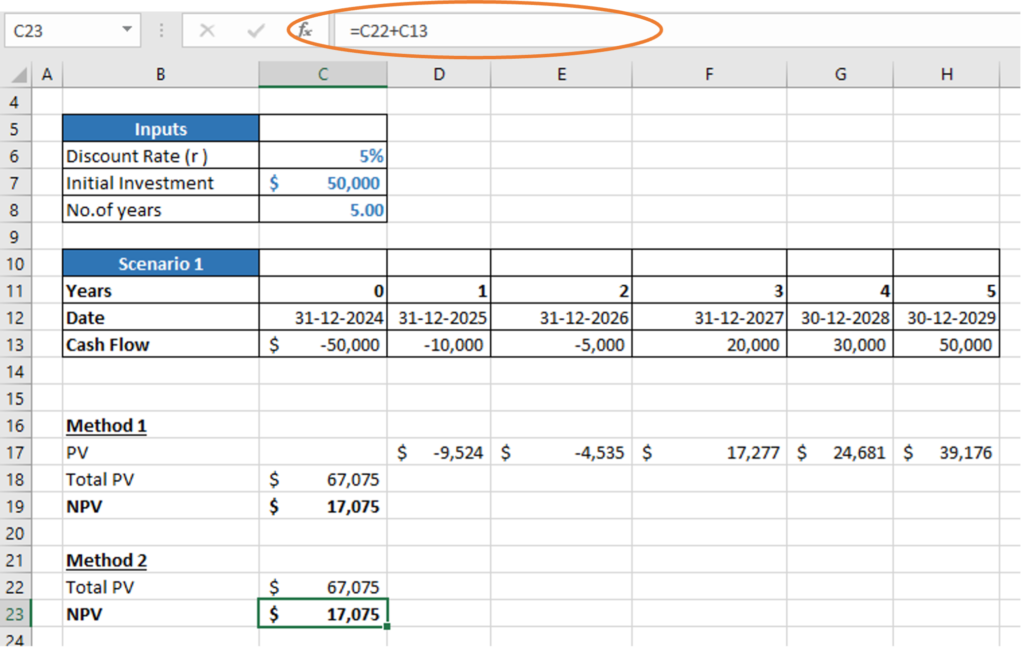
Method 2: Unlike Method 1, PV for all years can be calculated together using the NPV formula, where the user has to select the discount rate and range of cash flows. To calculate NPV, from the total PV calculated using the NPV formula, the user has to deduct the Initial investment made in the 0th year.
From below, we can see that the Total PV is calculated using the NPV formula in cell C22. The formula takes discount rate from cell C6 and cash flows from cell D13 to H13. From the Total PV we are deducting initial investment in cell C13 to arrive at NPV in cell C23.
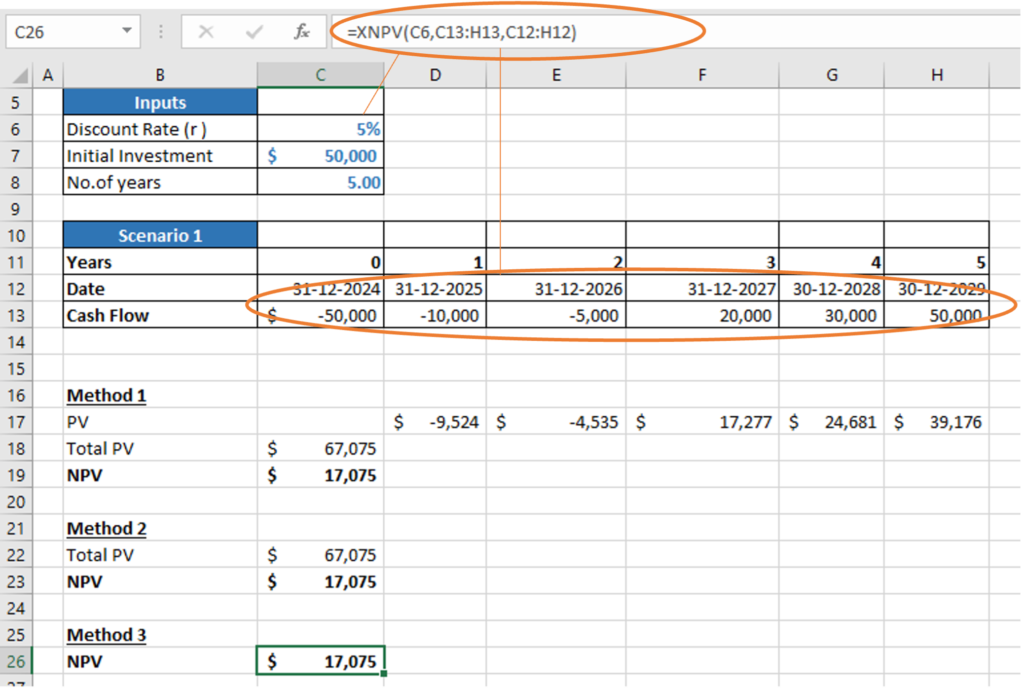
Method 3: Unlike both the methods above, in Method 3, the user can calculate NPV directly in a one-step formula named XNPV. In the formula, the user has to input the discount rate, the range of cash flows from the 0th year itself (in which investment is made), and the range of dates.
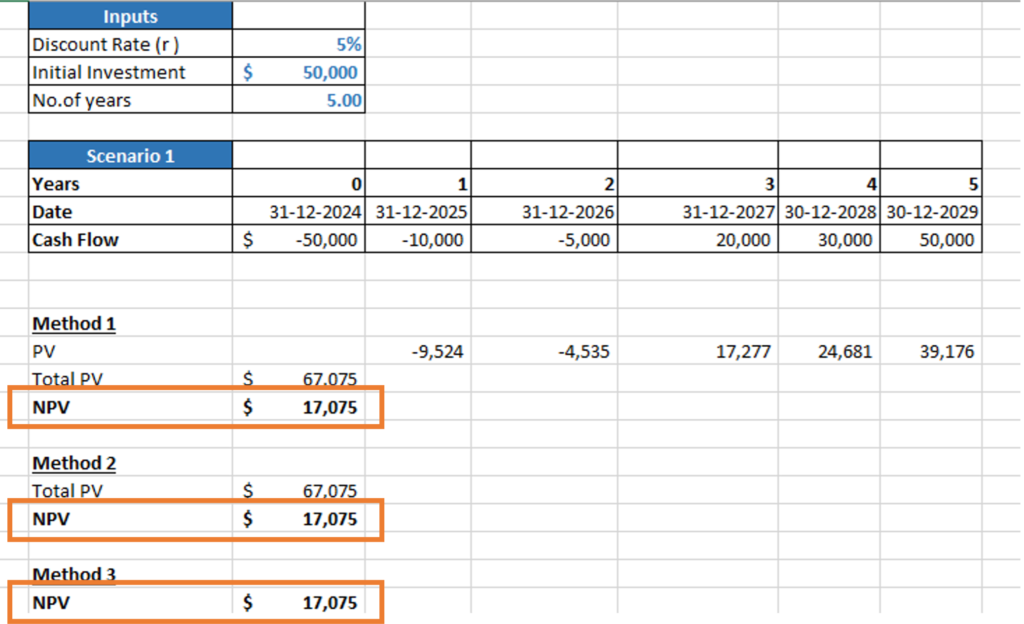
We get the same results using all three methods as below:
FINDING THE PRESENT VALUE OF FUTURE SERIES OF CASH FLOW INVOLVING EQUAL INSTALLMENTS
The PV function in Excel is a powerful tool for calculating the present value of a series of regular payments (PMT), such as annuities, loans, or lease payments. By inputting the payment amount (PMT), discount rate (rate), and number of periods (nper), the function determines the current worth of these future cash flows. This is particularly useful in practical scenarios like calculating the present value of a loan with fixed monthly payments, the value of a retirement annuity where regular amounts will be received, or lease agreements with consistent payments. For annuities, the PV function helps individuals and businesses assess the value today of regular income streams expected over time, enabling better financial planning and decision-making.
Let’s see an example below to understand the same.
Suppose we expect to receive $1,000 each year for the next 10 years, and we want to determine the current value of these payments given a 6% annual discount rate, compounded annually. To calculate this, you’ll use Excel’s PV function, which simplifies the process.
To calculate the present value of yearly payments using Excel, start by opening a worksheet and using the PV function to determine the current value of the series of future payments. In any cell, enter the PV function as follows:
=PV(rate, nper, pmt, [fv], [type])
Where,
- rate: 6%, representing the annual discount rate.
- nper: 10, as there are 10 yearly payments.
- pmt: -1000, representing the payment amount as a cash inflow (the negative sign indicates incoming cash).
- fv and type are optional, so you can leave them blank or set type to 0 to assume payments are made at the end of each period.
Press Enter, and Excel will calculate and display a result of approximately $7,360. This amount represents the present value of receiving $1,000 annually for 10 years at a 6% discount rate. This example shows how Excel’s PV function makes it simple to adapt calculations for different payment structures with a few straightforward inputs.
Below we have shown how Present value can be calculated for equal amounts of multiple cash flows over time in Excel using two methods.
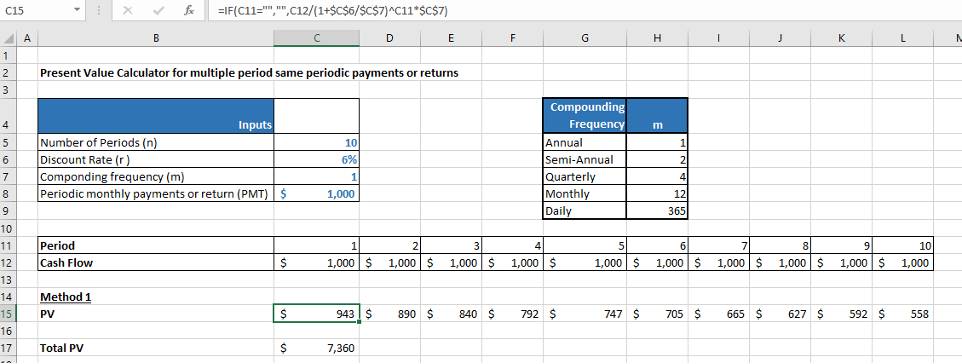
Method 1: Using the traditional DCF formula.
First PV is calculated for each year cash flow separately in cell C15 to cell L15. Then the Total PV is calculated in cell C17 as the sum of cell C15 to cell L15.
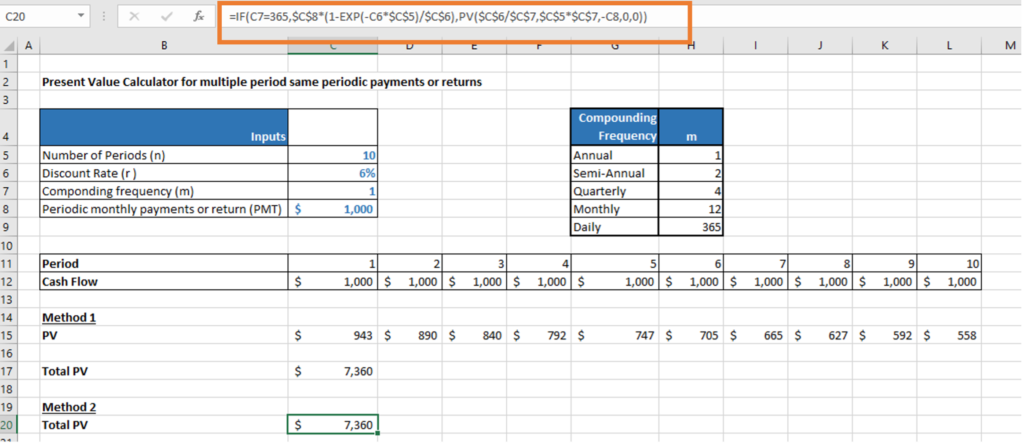
Method 2: Using PV function
The PV below is calculated by taking rate as 6%, time as 10 years and PMT as $1000, assuming annual compounding.
HOW DOES THE FREQUENCY OF COMPOUNDING IMPACT THE PRESENT VALUE?
Compounding significantly impacts the present value (PV) by influencing how future cash flows are discounted to their current worth. As interest is compounded more frequently, it increases the future value of cash flows by earning interest not only on the principal but also on accumulated interest. For instance, a $1,000 investment at 5% interest compounded quarterly yields slightly more than annual compounding. This higher future value amplifies the discounting effect when calculating PV, as the value of waiting for future cash flows becomes more pronounced. Additionally, compounding highlights the opportunity cost of capital—the returns foregone by delaying cash flows. Therefore, compounding enhances future cash flows and makes accurate present value calculations critical for evaluating the timing and opportunity cost of financial decisions.
Let’s see how compounding impacts the present value results below in case of Example 1 above, where you’re expecting to receive $1,000 in three years with a 6% discount rate. We use the following formula for Annual Compunding:
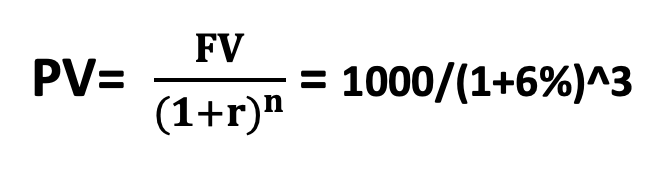
However, for the semi-annual compounding the formula becomes
For the above example, the formula for semi-annual compounding becomes PV= 1000/(1+6%/2)^3*2. We can create a table for different compounding frequency as shown
| Compounding Frequency | Annual | Semi-Annual | Quarterly | Monthly | Daily |
| PV | $ 839.62 | $ 837.48 | $ 836.39 | $ 835.64 | $ 835.27 |
| Interest (FV-PV) | $ 160.38 | $ 162.52 | $ 163.61 | $ 164.36 | $ 164.73 |
From above we can see that the interest earned is highest under the daily compounding.
Note: When the cash flow is compounded daily, the Formula to calculate PV where PV is
WHY USE A PRESENT VALUE CALCULATOR?
Calculating present value manually can be tedious, especially for complex cash flows or multiple future payments. This is where a Present Value calculator becomes invaluable. Here are a few reasons why these tools are widely used:
- Simplicity: PV calculators allow users to input variables easily without needing extensive mathematical knowledge. Just enter the future value, interest rate, and time period, and let the calculator do the work.
- Speed: Time is money. Present Value calculators provide instant results, saving valuable time for investors and analysts who may be working on multiple scenarios.
- Versatility: Many calculators offer options for different types of cash flows, including single lump sums or annuities (regular payments). This versatility makes them suitable for various financial analyses, from personal investments to corporate finance.
- Financial Decision-Making: By using a present value calculator, investors can make more informed decisions. It helps compare the attractiveness of different investment opportunities by understanding their current worth.
To simplify the Present Value and Net Present Value calculations we have attached an Excel calculator to perform calculations with a different set of inputs.
HOW IS PRESENT VALUE DIFFERENT FROM FUTURE VALUE?
When it comes to financial planning and investment decisions, the terms Present Value (PV) and Future Value (FV) often come up. While both concepts are rooted in the time value of money, they represent opposite sides of the equation.
Present Value (PV) is all about how much a future sum of money is worth today. It answers the question: What is the value of a future cash flow in today’s terms? Imagine we are about to receive $10,000 five years from now. If we want to know how much that’s worth today, given a 5% interest rate, we would calculate its present value. In this case, the PV would be roughly $7,835, meaning that’s the equivalent amount we would need to have in hand today to equal $10,000 in five years.
On the other hand, Future Value (FV) shows how much a sum of money today will be worth at a future date, factoring in growth from interest or returns. For example, if we invest $5,000 today at a 6% annual interest rate, in five years, it will grow to approximately $6,691. That’s the future value of our investment—what today’s cash will be worth after earning returns over time.
In essence, present value helps you assess the worth of future money today, while future value allows you to project how much today’s money will grow in the future. Both are crucial in making smart financial decisions, whether you’re investing for growth or planning to evaluate future cash flows.
HOW PRESENT VALUE IS RELATED TO THE TIME PERIOD AND DISCOUNT RATE?
The relationship between present value, time period, and discount rate highlights how the time value of money impacts financial decisions:
- Inverse Relationship with Time Period: As the time period increases, the present value decreases because future cash flows are discounted over a longer duration.
- Inverse Relationship with Discount Rate: A higher discount rate reduces the present value, as future cash flows are discounted more aggressively.
CONCLUSION
The present value theory is a direct application of the time value of money principle, emphasizing that money’s value changes over time due to its earning potential, risks, and opportunities. By understanding PV, individuals and businesses can make more informed financial decisions, ensuring that their investments are evaluated in light of their future worth. This alignment between the present value and the time value of money forms the backbone of sound financial analysis and decision-making.